FUNCIONES TRIGONOMÉTRICAS
Estimada alumna, si tenemos que realizar un análisis eficaz sobre funciones trigonométricas es necesario revisar algunos conceptos previos.
CONCEPTOS PREVIOS
RECORDEMOS:
FUNCIÓN: Una función es un conjunto no vacio de pares ordenados (x; y), no habiendo dos pares distintos con una misma primera componente
Las primeras componentes "x" de cada par conforman el DOMINIO de la función o D(f).
las segundas componentes "y" de cada par conforman el RANGO de la función o R(f)
GRAFICA DE UN FUNCIÓN:
La gráfica de una función es su representación geométrica en el plano cartesiano.
Ejemplos:
Una forma de observar mejor los pares correspondientes a una función consiste en escribir las componentes en un cuadro. Por ejemplo, en la función: y = 2x - 4
Si damos valores a x y los reemplazamos en la regla de correspondencia dada, obtenemos los valores respectivos para y, es decir:
En la tabla se puede observar, que al aumentar los valores de x; aumentan también los valores de y
Entonces decimos que dicha función es CRECIENTE
Una función es DECRECIENTE cuando al aumentar los valores de una variable, la otra disminuye y viceversa
FUNCIÓN CONTINUA Y FUNCIÓN DISCONTINUA
Una función es CONTINUA en un intervalo dado cuando al graficarla, el trazo correspondiente es ininterrumpido, es decir no presenta puntos de discontinuidad.
Una función es DISCONTINUA si la gráfica correspondiente presenta interrupciones, es decir; si tiene puntos en los cuales una pequeña variación de la variable independiente produce un salto en los valores de la variable dependiente. A estos puntos se les denomina puntos de discontinuidad.
Los puntos de discontinuidad pueden ser de dos tipos:
- Puntos en los que la función no está definida, es decir, los puntos que no pertenecen al dominio de la función, gráfica a.
- Puntos en los que la gráfica presenta un salto, gráfica b.
FUNCIÒN PAR Y FUNCIÓN IMPAR
En una función y = f(x)
Luego:
- f(-x) = f(x) en tal caso la función es PAR, o
- f(-x) = -f(x) en tal caso la función es impar
Ejemplos:
a)
b)
Ver video
FUNCIÓN PERIÓDICA
Una función es periódica si su gráfica, o las imágenes de los valores de x, se repiten cada cierto intervalo. A este intervalo del dominio o longitud del intervalo, T, se le llama período y significa que:
f(x) = f(x + T) = f(x + 2T) = ... = f(x + k · T), siendo k un número entero
Esto quiere decir que, conocido el valor de la función en un intervalo de amplitud T, se puede construir el resto de la gráfica trasladándola a la derecha y a la izquierda por todo el dominio de la función.
La gráfica de una función periódica es del tipo:
Ver Video
FUNCIÒN TRIGONOMÉTRICA
Las Rt que hemos estudiado relacionan un ángulo x con el seno, coseno, tangente, cotangente, secante y cosecante. esto hace que podamos hablar en adelante de FUNCIÓN TRIGONOMÉTRICA (Ft) en lugar de Rt. como en toda función consideraremos en el análisis: Dominio, rango, gráfica, creciniento o decrecimiento, continuidad o discontinuidad, si es par o impar, valores máximos/mínimos y periodo.
Las Razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.
Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones.
Se pueden definir geométricamente o por medio de sus relaciones. Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente; por ejemplo el verseno (1 − cos θ) y la exsecante (sec θ − 1).
| Función | Abreviatura | Equivalencias (en radianes) |
|---|---|---|
| Seno | sen (sin) | 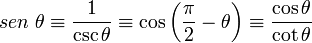 |
| Coseno | cos | 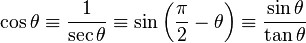 |
| Tangente | tan |  |
| Cotangente | cot | 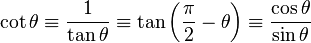 |
| Secante | sec |  |
| Cosecante | csc (cosec) |  |
Haz clic en los siguientes enlaces:
Espero que esta revisión de contenidos previos, aclare los conceptos básicos sobre funciones trigonométricas.









No hay comentarios:
Publicar un comentario